grdflexure

Compute flexural deformation of 3-D surfaces for various rheologies

Synopsis

gmt grdflexure input -Drm/rl[/ri]/rw[+rrr] -E[Te[k][/Te2[k]]] -Goutgrid [ -ANx/Ny/Nxy ] [ -Cp|yvalue ] [ -Fnu_a[/h_a[k]/nu_m] ] [ -Hrhogrid [ -Llist ] [ -Mtm ] [ -Nparams ] [ -Q ] [ -Sbeta ] [ -Tt0[/t1/dt[+l]]|file ] [ -V[level] ] [ -Wwd][k] [ -Zzm][k] [ -hheaders ] [ -fflags ] [ --PAR=value ]

Note: No space is allowed between the option flag and the associated arguments.

Description

grdflexure computes the deformation due to a topographic load \(h(\mathbf{x})\) for five different types of rheological foundations, all involving constant thickness thin plates:

1. An elastic plate overlying an inviscid half-space,

2. An elastic plate overlying a viscous half-space (Firmoviscous or Kelvin-Voigt),

3. An elastic plate overlying a viscous layer over a viscous half-space (Firmoviscous or Kelvin-Voigt),

4. A viscoelastic plate overlying an inviscid half-space (Maxwell solid),

5. A general linear viscoelastic model with an initial and final elastic plate thickness overlying an inviscid half-space.

These conditions will require the elastic [1; \(\Phi_e(\mathbf{k})\)], firmoviscous [2,3; \(\Phi_{fv}(\mathbf{k},t)\)], viscoelastic [4; \(\Phi_{ve}(\mathbf{k},t)\)], and general linear (viscoelastic) response functions [5; \(\Phi_{gl}(\mathbf{k},t)\)]. If the (visco)elastic plate vanishes (zero thickness) then we obtain Airy isostasy (1,4) or a purely viscous response (2,3). Temporal evolution can also be modeled by providing incremental load grids for select times and specifying a range of model output times. A wide range of options allows for specifying the desired rheology and related constants, including in-plate forces.

Required Arguments

input

Supplies the topographic load information in one of many forms:

• A single 2-D binary grid file with the topography of the load (in meters); (See Grid File Formats).

• If -T is used, input may be a filename template (See Name Template for details). The load times will thus coincide with the times given via -T (but not all times need to have a corresponding file).

• A file list given as flist+l, where flist is an ASCII table with one load time and topography grid filename per record (e.g., as produced by grdseamount -M). These load times can be different from the evaluation times given via -T. For load time format, see -T. Note: If flist has three trailing words the second will be interpreted as a load density grid name and used for that layer instead of the fixed rl setting in -D. The last trailing word is a formatted age string.

• A file list with extension “.lis” does not need the +l modifier and will be automatically recognized as a file list.

Note: The horizontal dimensions are expected to be in meters. If you have grids in km then you can append +uk to do the required conversion when the grid is read. All input grids must have the same dimensions. If a grid contains NaNs then they are quietly replaced with zeros; use -V to get a report when this happens.

-Drm/rl[/ri]/rw[+rrr]

Sets density for mantle, load, infill, and water (or air). If ri differs from rl then an approximate solution will be found. If ri is not given then it defaults to rl. Values may be given in \(\mbox{kg/m}^3\) or \(\mbox{g/cm}^3\). Note: If a variable load density grid is supplied via -H then rl must be given as -. Whether the load density is variable or not, you can (via the +r modifier) specify a fixed root density, i.e., the infill density just beneath the load. This will force the load topography to be rescaled by the ratio rl/rr and then rl will be reset to rr for flexure calculations.

-E[Te[k][/Te2[k]]

Sets the elastic plate thickness (in meter); append k for km. If the elastic thickness exceeds 1e10 it will be interpreted as a flexural rigidity D (by default, D is computed from Te, Young’s modulus, and Poisson’s ratio; see -C to change these values). If -E is given with no arguments and -F is given it means no plate is present and we will return a purely viscous response with or without an asthenospheric layer. Select a general linear viscoelastic response instead by supplying both an initial and final elastic thickness Te2; this response also requires -M.

-Goutgrid[=ID][+ddivisor][+ninvalid][+ooffset|a][+sscale|a][:driver[dataType][+coptions]]

Optionally, append =ID for writing a specific file format. The following modifiers are supported:

• +d - Divide data values by given divisor [Default is 1].

• +n - Replace data values matching invalid with a NaN.

• +o - Offset data values by the given offset, or append a for automatic range offset to preserve precision for integer grids [Default is 0].

• +s - Scale data values by the given scale, or append a for automatic scaling to preserve precision for integer grids [Default is 1].

Note: Any offset is added before any scaling. +sa also sets +oa (unless overridden). To write specific formats via GDAL, use =gd and supply driver (and optionally dataType) and/or one or more concatenated GDAL -co options using +c. See the “Writing grids and images” cookbook section for more details.

Optional Arguments

-ANx/Ny/Nxy

Specify in-plane compressional or extensional forces in the x- and y-directions, as well as any shear force [no in-plane forces]. Compression is indicated by negative values, while extensional forces are specified using positive values. Values are expected in Pa·m since N is the depth-integrated horizontal stresses.

-Cp|yvalue

Append directives p or y to change the current value of Poisson’s ratio [0.25] or Young’s modulus [7.0e10 N/m²], respectively.

-Fnu_a[/h_a[k]/nu_m]

Specify a firmoviscous model in conjunction with an elastic plate thickness specified via -E. Just give one viscosity (nu_a) for an elastic plate over a viscous half-space, or also append the thickness of the asthenosphere (h_a) and the lower mantle viscosity (nu_m), with the first viscosity now being that of the asthenosphere. Give viscosities in Pa·s. If used, give the thickness of the asthenosphere in meter; append k for km. Cannot be used in conjunctions with -M.

-Hrhogrid

Supply optional variable load density grid. It can be a single grid or a grid name template (see Name Template for details). Requires rho_l be set to - in -D. The density grid may be NaN at nodes where the load grid is NaN (or zero). Note: If input is given as a list file then the optional density grids must be given as part of the list and not via -H.

-Llist

Write the names and evaluation times of all grids that were created to the text file list. Requires -T. The leading numerical column will be time in years, while the last trailing text word is formatted time. The output records thus contain time flexuregrid timetag.

-Mtm

Specify a viscoelastic model in conjunction with a plate thickness specified via -E. Append the Maxwell time tm for the viscoelastic model (in years); add k for kyr and M for Myr. Cannot be used in conjunctions with -F.

-N[a|f|m|r|s|nx/ny][+a|d|h|l][+e|n|m][+twidth][+v][+w[suffix]][+z[p]]

Choose or inquire about suitable grid dimensions for FFT and set optional parameters. Control the FFT dimension via these directives:

• a - Let the FFT select dimensions yielding the most accurate result.

• f - Force the FFT to use the actual dimensions of the data.

• m - Let the FFT select dimensions using the least work memory.

• r - Let the FFT select dimensions yielding the most rapid calculation.

• s - Just present a list of optional dimensions, then exit.

Without a directive we expect -Nnx/ny which will do FFT on array size nx/ny (must be >= grid file size). Default chooses dimensions >= data which optimize speed and accuracy of FFT. If FFT dimensions > grid file dimensions, data are extended and tapered to zero.

Control detrending of data by appending a modifier for removing a linear trend. Consult module documentation for the default action:

• +d - Detrend data, i.e. remove best-fitting linear trend.

• +a - Only remove the mean value.

• +h - Only remove the mid value, i.e. 0.5 * (max + min).

• +l - Leave data alone.

Control extension and tapering of data by appending a modifier to control how the extension and tapering are to be performed:

• +e - Extend the grid by imposing edge-point symmetry [Default].

• +m - Extends the grid by imposing edge mirror symmetry.

• +n - Turns off data extension.

Tapering is performed from the data edge to the FFT grid edge [100%]. Change this percentage via modifier +twidth. When +n is in effect, the tapering is applied instead to the data margins as no extension is available [0%].

Control messages being reported:

• +v - Report suitable dimensions during processing.

Control writing of temporary results: For detailed investigation you can write the intermediate grid being passed to the forward FFT; this is likely to have been detrended, extended by point-symmetry along all edges, and tapered. Use these modifiers to ave such grids:

• +w - Set the suffix from which output file name(s) will be created (i.e., ingrid_prefix.ext) [Default is “tapered”], where ext is your file extension

• +z - Save the complex grid produced by the forward FFT. By default we write the real and imaginary components to ingrid_real.ext and ingrid_imag.ext. Append p to instead use the polar form of magnitude and phase to files ingrid_mag.ext and ingrid_phase.ext.

-Q

Do not make any flexure calculations but instead take the chosen response function given the parameters you selected and evaluate it for a range of wavenumbers and times; see the note on transfer functions below.

-Sbeta

Specify a starved moat fraction in the 0-1 range, where 1 means the moat is fully filled with material of density ri while 0 means it is only filled with material of density rw (i.e., just water) [1].

-Tt0[/t1/dt[+l]]|file

Specify t0, t1, and time increment (dt) for a sequence of calculations [Default is one calculation, with no time dependency]. For a single specific time, just give start time t0. Default unit is years; append k for kyr and M for Myr. For a logarithmic time scale, append +l and specify n steps instead of dt. Alternatively, give a file with the desired times in the first column (these times may have individual units appended, otherwise we assume year). We then write a separate model grid file for each given time step; see -G for output and Name Template for the file template format.

-V[level]

Select verbosity level [w]. (See full description) (See technical reference).

-Wwd[k]

Specify water depth in m; append k for km. Must be positive [0]. Any subaerial topography (i.e., amplitudes in the input relief that exceeds this depth) will be scaled via the densities set in -D to compensate for the larger density contrast with air.

-Zzm[k]

Undeformed plate flexure means z = 0. Specify the distance between the observation level [z = 0] and the undeformed flexed surface in m; append k for km. Must be positive [0]. We subtract this value from the flexed surface before output. Thus, if the observation level is at sealevel and you are looking a seafloor deformation in 5 km of water, use -Z5k and the undeformed surface will have z = -5000 on output.

-fflags

Geographic grids (dimensions of longitude, latitude) will be converted to meters via a “Flat Earth” approximation using the current ellipsoid parameters.

-h[i|o][n][+c][+d][+msegheader][+rremark][+ttitle] (more …)

Skip or produce header record(s).

-^ or just -

Print a short message about the syntax of the command, then exit (Note: on Windows just use -).

-+ or just +

Print an extensive usage (help) message, including the explanation of any module-specific option (but not the GMT common options), then exit.

-? or no arguments

Print a complete usage (help) message, including the explanation of all options, then exit.

--PAR=value

Temporarily override a GMT default setting; repeatable. See gmt.conf for parameters.

Name Template

The format statements allowed in grid file templates require you to follow these rules:

• To use the formatted time-tag as part of the file name you must use just a single %s format as part of the template (e.g., smt_%s.grd).

• If you want to control the numerical formatting of the names but still have the common time unit appended then you must compose a template that has a floating point format before a later %c format for the unit. For example, smt_%05.1f%c.grd will create names like smt_001.1M.grd names. The times will be scaled to match the unit.

• If you do not want any units then simply give a template with just one floating point format, e.g., smt_%05.1f_name.grd. The times will be used as is (i.e, unscaled).

For details on the format statements, see printf C language format syntax.

Grid Distance Units

If a Cartesian grid does not have meter as the horizontal unit, append +uunit to the input file name to convert from the specified unit to meter. E.g., appending +uk to the load file name will scale the grid x, y coordinates from km to meter. If your grid is geographic, convert distances to meters by supplying -fflags instead. netCDF COARDS geographic grids will automatically be recognized as geographic.

Considerations

The calculations are done using a rectangular Cartesian FFT operation. If your geographic region is close to either pole, you should consider using a Cartesian setup instead; you can always project it back to geographic using grdproject.

Data Detrending

The default detrending mode is to remove a best-fitting linear plane (+d). Consult and use -N to select other modes.

Transfer Functions

If -Q is given we perform no actual flexure calculations and no input data file is required. Instead, we write the chosen transfer functions \(\Phi(\mathbf{k},t)\) to 7 separate files for 7 different Te values (1, 2, 5, 10, 20, 50, and 100 km). The first two columns are always wavelength in km and wavenumber (in 1/m) for a 1:1:3000 km range. The transfer functions are evaluated for 12 different response times: 1k, 2k, 5k, 10k, 20k, 50k, 100k, 200k, 500k, 1M, 2M, and 5M years. For a purely elastic response function we only write the transfer function once per elastic thickness (in column 3). The 7 files are named grdflexure_transfer_function_te_te_km.txt, where te is replaced by the 7 elastic thicknesses in km (and 0 if -E[0] was used for a viscous response only).

Examples

We will use a Gaussian seamount load to demonstrate grdflexure. First, we make a grid of for that shape by placing a Gaussian truncated seamount at position (300,300) with a radius of 50 km and height of 5000 m:

echo 300 300 0  40  40  5000 | gmt grdseamount -R0/600/0/600+uk -I1000 -Gsmt.nc t.txt -Dk -E -F0.1 -Cg

To compute elastic plate flexure from the load smt.nc, for a 10 km thick plate with typical densities, try:

gmt grdflexure smt.nc -Gflex.nc -E10k -D2700/3300/1035

To see how in-plane stresses affect the result, we use -A. Remember that we need to depth- integrated forces, not pressures, hence we try:

gmt grdflexure smt.nc -Gflex.nc -E10k -D2700/3300/1035 -A-4e11/2e11/-1e12

To compute viscoelastic plate flexure from the load smt.nc, for a 20 km thick plate with typical densities and a Maxwell time of 40kyr, try:

gmt grdflexure smt.nc -Gflex.nc -E20k -D2700/3300/1035 -M40k

To compute firmoviscous plate flexure from the load smt.nc, for a 15 km thick plate with typical densities overlying a viscous mantle with viscosity 2e21, try:

gmt grdflexure smt.nc -Gflex.nc -E15k -D2700/3300/1035 -F2e21

To compute the general linear viscoelastic plate flexure from the load smt.nc, for an initial Te of 40 km and a final Te of 15 km with typical densities and a Maxwell time of 100 kyr, try:

gmt grdflexure smt.nc -Gflex.nc -E40k/15k -D2700/3300/1035 -M100k

To just compute the firmoviscous response functions using the specified rheological values, try:

gmt grdflexure -D3300/2800/2800/1000 -Q -F2e20

The following are not user-reproducible but shows the kind of calculations that can be done. To compute the firmoviscous response to a series of incremental loads given by file name and load time in the table l.lis at the single time 1 Ma using the specified rheological values, try:

gmt grdflexure -T1M =l.lis -D3300/2800/2800/1000 -E5k -Gflx/smt_fv_%03.1f_%s.nc -F2e20 -Nf+a

Theory of Response Functions

Deformation \(w(\mathbf{x})\) caused by topography \(h(\mathbf{x})\) applied instantaneously to the rheological foundation at time t = 0 and evaluated at a later time t is given in the Fourier domain by

\[W(\mathbf{k},t) = \gamma \left (\frac{\rho_l - \rho_w}{\rho_m - \rho_l} \right ) H(\mathbf{k}) \Phi(\mathbf{k},t) = \gamma A H(\mathbf{k}) \Phi(\mathbf{k},t),\]

where \(\mathbf{k} = (k_x, k_y)\) is the wavenumber vector, \(k_r\) its magnitude, \(H(\mathbf{k})\) is the topographic load in the wavenumber domain, A is the Airy density ratio, \(\gamma\) is a constant that depends on the infill density, and \(\Phi(\mathbf{k},t)\) is the response function for the selected rheology. The grdflexure module read one or more loads h, transforms them to H, evaluates and applies the response function, and inversely transform the results back to yield on or more w solutions.

Variable load density

If the load density is variable (i.e., provided as a grid via -H) then we simply adjust the load height to be the equivalent height for the average load density. This is accomplished on a node-by-node basis by honoring the equality \(\rho_l(\mathbf{x})\cdot h(\mathbf{x}) = \bar{\rho_l}\cdot h'(\mathbf{x})\), where the prime height is the adjusted amplitude.

Submarine and subaerial loads

If the water depth is specified via -W then we check if the (possibly adjusted) load height exceeds the water depth for any node. If so, then we adjust the load height that is above water to what it needs to be if the density contrast were against water and not air. The subaerial height component is thus extended by \(\frac{\rho_l}{\rho_l - \rho_w}\).

Variable infill approximation

If \(\rho_i = \rho_l\) then \(\gamma = 1\), otherwise the infill density varies spatially and the Fourier solution is not valid. We avoid these complications by letting \(\rho_l = \rho_i\) and increasing the deformation amplitude by

\[\gamma = \sqrt{\frac{\rho_m - \rho_i}{\rho_m - \rho_l}}.\]

The approximation is good except for very large loads on thin plates (Wessel, 2001).

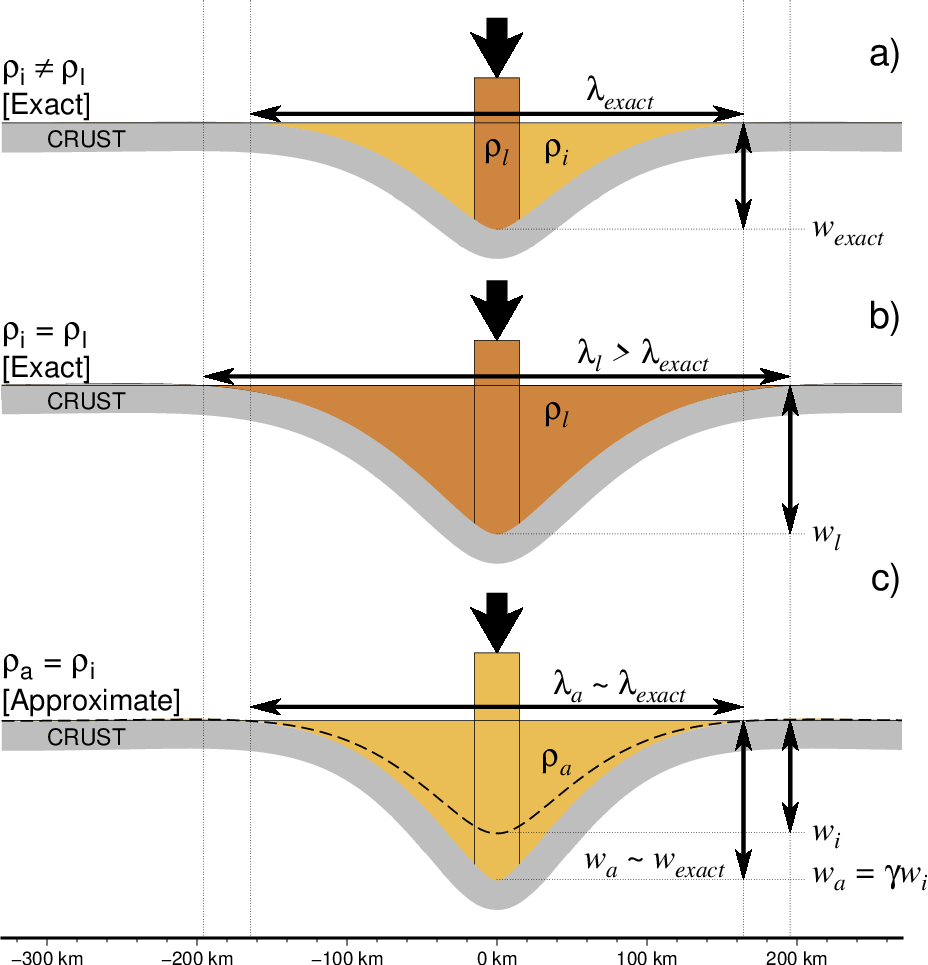
a) We want a flexural calculation that allows for different densities in the moat (\(\rho_i\)) and beneath the load (\(\rho_l\)). Unfortunately, the Fourier method requires a constant density contrast. b) Reusing the load density as a (higher) infill density gives an exact answer, but overestimates both the flexural wavelength (\(\lambda_l\)) and the amplitude of deflection (\(w_l\)). c) Reusing the infill density as a (lower) load density gives approximately the correct flexural wavelength but underestimates the amplitude (dashed curve). We achieve a satisfactory approximation by scaling \(w_i\) by the factor \(\gamma\) (modified from Wessel [2016]).

Elastic response function

The time-independent elastic response function is

\[\Phi_e(\mathbf{k}) = \left [ 1 + \alpha_r^4 + \epsilon_x \alpha_x^2 + \epsilon_y \alpha_y^2 + \epsilon_{xy} \alpha_{xy}^2 \right ]^{-1}, \quad \alpha_s = k_s / k,\]

where the flexural wavenumber k and constants \(\epsilon_s\) via in-plane stresses \(N_x, N_y, N_{xy}\) are

\[k = \left [ \frac{(\rho_m - \rho_i)g}{D} \right ]^{\frac{1}{4}}, \quad \epsilon_s = \left [ \frac{N_s}{(\rho_m - \rho_i)g} \right ]^{\frac{1}{2}},\]

for subscripts \(s = \left (x, y, xy \right )\). In the most common scenario, \(N_s\) are all zero and the elastic response function becomes isotropic:

\[\Phi_e(k_r) = \left [ 1 + \alpha_r^4 \right ]^{-1}.\]

Firmoviscous response function

The firmoviscous response function \(\Phi(\mathbf{k},t)\) scales the magnitude of the deformation at a given wavenumber and time and depends on rheological parameters and in-plane stresses:

\[\Phi_{fv}(\mathbf{k},t) = \Phi_e(\mathbf{k}) \left [ 1 - \exp \left \{ - \frac{(\rho_m - \rho_l) \tau(k_r)}{\rho_m\Phi_e(\mathbf{k})} t \right \} \right ].\]

If the foundation is an inviscid half-space, then the relaxation parameter \(\tau(k_r) = \infty\), there is no time-dependence, and \(\Phi_{fv}(\mathbf{k},t) = \Phi_e(\mathbf{k})\). Otherwise, it is given by

\[\tau(k_r) = \frac{\rho_m g}{2 \eta_m k_r} \beta(k_r),\]

where \(\beta(k_r)\) depends on whether we have a finite-thickness layer of thickness \(T_a\) and viscosity \(\eta_a\) above the half-space of viscosity \(\eta_m\) (Cathles, 1975; Nakada, 1986). If no finite layer exists then \(\beta(k_r) = 1\), otherwise

\[\beta(k_r) = \frac{(\theta + \theta^{-1}) CS + k_r T_a (\theta - \theta^{-1}) + S^2 + C^2}{2CS\theta + (1-\theta)k_r^2 T_a^2 + \theta S^2 + C^2},\]

where

\[\theta = \eta_a/\eta_m, \quad S = \sinh (k_r T_a), \quad C = \cosh (k_r T_a).\]

Airy and viscous response function

In the limit \(t \rightarrow \infty, \tau \rightarrow 0\) and we approach the purely elastic solution

\[W(\mathbf{k}) = A \gamma H(\mathbf{k}) \Phi_e(\mathbf{k}).\]

Otherwise, if the plate has no strength (-E0), then \(\Phi_e(\mathbf{k}) = 1\) and the response function is purely viscous and isotropic:

\[\Phi_v(k_r,t) = \left [ 1 - \exp \left \{ - \frac{(\rho_m - \rho_l) \tau(k_r)}{\rho_m} t \right \} \right ].\]

For \(t \rightarrow \infty\) (or for an inviscid half-space) we approach Airy isostasy: \(w(\mathbf{x}) = A h(\mathbf{x})\).

Maxwell viscoelastic response

For case (4), the viscoelastic response function (only available for an inviscid substratum) is

\[\Phi_{ve}(\mathbf{k},t) = 1 - \left [ 1 - \Phi_e(\mathbf{k}) \right ] \exp \left \{ - \frac{t}{t_m} \Phi_e(\mathbf{k}) \right \},\]

where \(t_m\) is the Maxwell relaxation time (Watts, 2001).

General linear viscoelastic response

For case (5), the general linear viscoelastic response function (with an inviscid substratum) is (Karner, 1982)

\[\Phi_{gl}(\mathbf{k},t) = \Phi_f(\mathbf{k}) + \left [ \Phi_i(\mathbf{k}) - \Phi_f(\mathbf{k}) \right ] \exp \left \{ - \frac{t}{t_m} \frac{D_i \Phi_i(\mathbf{k})}{D_f \Phi_f(\mathbf{k})} \right \},\]

where subscripts i and f refers to the initial (t = 0) and final (\(t = \infty\)) values for rigidities (\(D_i, D_f\)) and elastic response functions (\(\Phi_i, \Phi_f\)).

References

Cathles, L. M., 1975, The viscosity of the earth’s mantle, Princeton University Press.

Karner, G. D., 1982, Spectral representation of isostatic models, BMR J. Australian Geology & Geophysics, 7, 55-62.

Nakada, M., 1986, Holocene sea levels in oceanic islands: Implications for the rheological structure of the Earth’s mantle, Tectonophysics, 121, 263–276, https://doi.org/10.1016/0040-1951(86)90047-8.

Watts, A. B., 2001, Isostasy and Flexure of the Lithosphere, 458 pp., Cambridge University Press.

Wessel. P., 2001, Global distribution of seamounts inferred from gridded Geosat/ERS-1 altimetry, J. Geophys. Res., 106(B9), 19,431-19,441, https://doi.org/10.1029/2000JB000083.

Wessel, P., 2016, Regional–residual separation of bathymetry and revised estimates of Hawaii plume flux, Geophys. J. Int., 204(2), 932-947, https://doi.org/10.1093/gji/ggv472.

See Also

gmt, gmtflexure, grdfft, gravfft, grdmath, grdproject, grdseamount