grdvector
Plot vector field from two component grids
Synopsis
gmt grdvector compx.nc compy.nc -Jparameters [ -A ] [ -B[p|s]parameters ] [ -Ccpt ] [ -Gfill ] [ -I[x]dx[/dy] ] [ -K ] [ -N ] [ -O ] [ -P ] [ -Qparameters ] [ -Rregion ] [ -S[i|l]scale ] [ -T ] [ -U[stamp] ] [ -Wpen ] [ -X[a|c|f|r][xshift] ] [ -Y[a|c|f|r][yshift] ] [ -Z ] [ -fflags ] [ -pflags ] [ -ttransp ] [ --PAR=value ]
Description
grdvector reads two 2-D grid files which represents the x- and y-components, \((x,y)\), of a vector field and produces a vector field plot by drawing vectors with orientation and length according to the information in the files. Alternatively, polar coordinate grids, \((r,\theta)\), may be given instead (see -A and -Z).
Required Arguments
- grid1
Contains the x-components of the vector field. (See Grid File Formats).
- grid2
Contains the y-components of the vector field. (See Grid File Formats).
Order is important. For \((x,y)\), grid1 is expected to be the x-component, and grid2 to be the y-component. For \((r,\theta)\), grid1 is expected to be the magnitude (\(r\)), and grid2 (\(\theta\)), to be the azimuth (-Z) or direction (-A).
- -Jparameters
Specify the projection. (See full description) (See technical reference) (See projections table).
Optional Arguments
- -A
The grid files contain polar \((r,\theta)\) components (magnitude and direction) instead of Cartesian \((x,y)\) [Default is Cartesian components]. If \(\theta\) contains azimuth, see -Z.
- -B[p|s]parameters
Set map boundary frame and axes attributes. (See full description) (See technical reference).
- -C[section/]master|cpt|color\(_1\),color\(_2\)[,color\(_3\),…][+h[hinge]][+idz][+u|Uunit][+sfname]
Name of a master CPT, an input CPT file or a comma-separated list of colors from which to build a CPT. If no argument is given then under modern mode we select the current CPT, if it is available. Generally, the input can be many things:
A standard GMT master CPT file, e.g., earth (see Of Colors and Color Legends) and can be either addressed by master or section/master (without any .cpt extension).
File name of already custom-made cpt file (e.g, my_colors.cpt).
Build a linear continuous CPT from color\(_1\),color\(_2\)[,color\(_3\),…] automatically, where z starts at 0 and is incremented by one for each color. In this case, color\(_i\) can be a r/g/b (e.g., 255/100/75), h-s-v triplet (e.g., 180-0.8-1), a c/m/y/k quadruple (e.g., 80/50/40/30), an HTML hexadecimal color (e.g. #aabbcc), or a color name. No spaces between commas are allowed.
A few modifiers pertains to hinges and units:
+h - If given a master CPT with soft hinges then you can enable the hinge at data value hinge [0], whereas for hard-hinge CPTs you can adjust the location of the hinge [0] but not disable it.
+i - Append increment dz to quantize the grid range [Default uses the exact grid range].
+s - Append fname to save the finalized CPT in a disk file. This is useful when the CPT is generated automatically, but if used, must be at the end of the -C option.
+u - For any other master CPT, you may convert their z-values from other distance Units to meter by appending the original unit code.
+U - Likewise, you may convert their z-values from meter to other Units by appending the desired unit code.
- -Gfill
Sets color or shade for vector interiors [Default is no fill]. Alternatively, the fill may be set via -Q.
- -I[x]dx[/dy]
Only plot vectors at nodes every x_inc, y_inc apart (must be multiples of original grid spacing). Append m for arc minutes or s for arc seconds. Alternatively, use -Ix to specify the multiples multx[/multy] directly [Default plots every node].
- -N
Do not clip vectors at map boundaries [Default will clip].
- -Qparameters
Modify vector parameters. For vector heads, append vector head size [Default is 0, i.e., stick-plot]. See Vector Attributes for specifying additional attributes.
- -Rxmin/xmax/ymin/ymax[+r][+uunit]
Specify the region of interest. Specify a subset of the grid. (See full description) (See technical reference).
- -S[i|l]scale[+c[[slon/]slat]][+srefsize]
Sets scale for vector plot lengths in data units per plot distance measurement unit. Append c, i, or p to indicate the desired plot distance measurement unit (cm, inch, or point); if no unit is given we use the default value that is controlled by PROJ_LENGTH_UNIT. Vector lengths converted via plot unit scaling will plot as straight Cartesian vectors and their lengths are not affected by map projections and coordinate locations. For geographic data you may alternatively give scale in data units per map distance unit (see Units). Then, your vector magnitudes (in data units) are scaled to map distances in the given distance unit, and finally projected onto the Earth to give plot dimensions. These are geo-vectors that follow great circle paths and their lengths may be affected by the map projection and their coordinates. Finally, use -Si if it is simpler to give the reciprocal scale in plot length or distance units per data unit. Alternatively, use -Sllength to set a fixed plot length for all vectors. To report the minimum, maximum, and mean data and plot vector lengths of all vectors plotted, use -V. If an automatic legend entry is desired via -l, one or two modifiers will be required:
+c[[slon/]slat] controls where on a geographic map a geovector’s refsize length applies. The modifier is neither needed nor available when plotting Cartesian vectors. The length is calculated for latitude slat (optionally supply longitude slon for oblique projections [default is central meridian]). If +c is given with no arguments then we select the reference length origin to be the middle of the map.
+srefsize sets the desired reference vector magnitude in data units. E.g., for a reference length of 25 mm/yr for plate motions, use modifier +s25 with a corresponding option -l“Velocity (25 mm/yr)”. If refsize is not specified we default to the scale given above.
- -T
Means the azimuths of Cartesian data sets should be adjusted according to the signs of the scales in the x- and y-directions [Leave alone]. This option can be used to convert vector azimuths in cases when a negative scale is used in one of both directions (e.g., positive down).
- -U[label|+c][+jjustify][+odx[/dy]][+ttext]
Draw GMT time stamp logo on plot. (See full description) (See technical reference).
- -V[level]
Select verbosity level [w]. (See full description) (See technical reference).
- -Wpen[+c]
Change the pen attributes used for vector outlines [Default: width = default, color = black, style = solid]. If the modifier +c is appended then the color of the vector head and stem are taken from the CPT (see -C).
- -X[a|c|f|r][xshift]
Shift plot origin. (See full description) (See technical reference).
- -Y[a|c|f|r][yshift]
Shift plot origin. (See full description) (See technical reference).
- -Z
The \(\theta\) grid provided contains azimuth (in degrees east of north) rather than direction (in degrees counter-clockwise from horizontal). Implies -A.
- -f[i|o]colinfo (more …)
Specify data types of input and/or output columns.
- -l[label][+Dpen][+Ggap][+Hheader][+L[code/]txt][+Ncols][+Ssize[/height]][+V[pen]][+ffont][+gfill][+jjust][+ooff][+ppen][+sscale][+wwidth] (more …)
Add a legend entry for the symbol or line being plotted.
- -p[x|y|z]azim[/elev[/zlevel]][+wlon0/lat0[/z0]][+vx0/y0] (more …)
Select perspective view.
- -ttransp[/transp2] (more …)
Set transparency level(s) in percent.
- -^ or just -
Print a short message about the syntax of the command, then exit (Note: on Windows just use -).
- -+ or just +
Print an extensive usage (help) message, including the explanation of any module-specific option (but not the GMT common options), then exit.
- -? or no arguments
Print a complete usage (help) message, including the explanation of all options, then exit.
- --PAR=value
Temporarily override a GMT default setting; repeatable. See gmt.conf for parameters.
Units
For map distance unit, append unit d for arc degree, m for arc minute, and s for arc second, or e for meter [Default unless stated otherwise], f for foot, k for km, M for statute mile, n for nautical mile, and u for US survey foot. By default we compute such distances using a spherical approximation with great circles (-jg) using the authalic radius (see PROJ_MEAN_RADIUS). You can use -jf to perform “Flat Earth” calculations (quicker but less accurate) or -je to perform exact geodesic calculations (slower but more accurate; see PROJ_GEODESIC for method used).
Vector Attributes
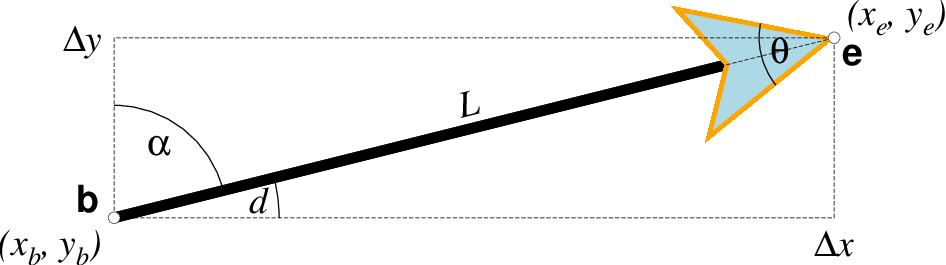
Vector attributes are controlled by options and modifiers. We will refer to this figure and the labels therein when introducing the corresponding modifiers. All vectors require you to specify the begin point \(x_b, y_b\) and the end point \(x_e, y_e\), or alternatively the direction d and length L, while for map projections we usually specify the azimuth \(\alpha\) instead.
Several modifiers may be appended to vector-producing options for specifying the placement of vector heads, their shapes, and the justification of the vector. Below, left and right refers to the side of the vector line when viewed from the beginning point (b) to the end point (e) of a line segment:
+a - Append argument to set the angle \(\theta\) of the vector head apex [30].
+b - Place a vector head at the beginning of the vector path [none]. Optionally, append t for a terminal line, c for a circle, s for a square, a for arrow [Default], i for tail, A for plain open arrow, and I for plain open tail. Note: For geovectors only a and A are available. Further append l|r to only draw the left or right half-sides of this head [both sides].
+c - Select the vector data quantity magnitude for use with CPT color look-up [Default requires a separate data column following the 2 or 3 coordinates]. Requires that data quantity scaling (with unit q via +v or +z) and a CPT have been selected.
+e - Place a vector head at the end of the vector path [none]. Optionally, append t for a terminal line, c for a circle, s for a square, a for arrow [Default], i for tail, A for plain open arrow, and I for plain open tail. Note: For geovectors only a and A are available. Further append l|r to only draw the left or right half-sides of this head [both sides].
+g - Append [fill] sets the vector head fill [Default fill is used, which may be no fill]. Turn off vector head fill by not appending a fill. Some modules have a separate -Gfill option and if used will select the fill as well.
+h Append shape of the vector head (range -2/2). Default is controlled by MAP_VECTOR_SHAPE [default is theme dependent]. A zero value produces no notch. Positive values moves the notch toward the head apex while a negative value moves it away. The example above uses +h0.5.
+m - Places a vector head at the mid-point the vector path [none]. Append f or r for forward or reverse direction of the vector [forward]. Optionally, append t for a terminal line, c for a circle, a for arrow [Default], i for tail, A for plain open arrow, and I for plain open tail. Further append l|r to only draw the left or right half-sides of this head [both sides]. Cannot be combined with +b or +e.
+n - Give [norm[/min]] to scale down vector attributes (pen thickness, head size) with decreasing length, where vector plot lengths shorter than norm will have their attributes scaled by length/norm [other arrow attributes remain invariant to length]. Optionally, append /min for the minimum shrink factor (in the 0-1 range) that we will shrink to [0.25]. For Cartesian vectors, please specify a norm in plot units, while for geovectors specify a norm in map units (see Distance units) [k]. Alternatively, append unit q to indicate we should use user quantity units in making the decision; this means the user also must select user quantity input via +v or +z. If no argument is given then +n ensures vector heads are not shrunk and always plotted regardless of vector length [Vector heads are not plotted if exceeding vector length].
+o - Specify the oblique pole [plon/plat] for the great or small circles. Only needed for great circles if +q is given. If no pole is appended then we default to the north pole. Input arguments are then lon lat arclength with the latter in map distance units; see +q of angular limits instead.
+p - Sets the vector pen attributes [pen]. If no pen is appended then the head outline is not drawn. [Default pen is half the width of stem pen, and head outline is drawn]. Above, we used +p2p,orange. The vector stem attributes are controlled by -W.
+q - Means the input direction, length data instead represent the start and stop opening angles of the arc segment relative to the given point. See +o to specify a specific pole for the arc [north pole].
+t[b|e]trim - Shift the beginning or end point (or both) along the vector segment by the given trim; append suitable unit (c, i, or p). If the modifiers b|e are not used then trim may be two values separated by a slash, which is used to specify different trims for the beginning and end. Positive trims will shorted the vector while negative trims will lengthen it [no trim].
In addition, all but circular vectors may take these modifiers:
+j - The just determines how the input x,y point relates to the vector. Choose from beginning [default], end, or center.
+s - The input angle, length are instead the \(x_e, y_e\) coordinates of the vector end point.
Finally, Cartesian vectors and geovectors may take these modifiers (except in grdvector) which can be used to convert vector components to polar form or magnify user quantity magnitudes into plot lengths:
+v[i|l]scale - Expects a scale to magnify the polar length in the given unit. If i is prepended we use the inverse scale while if l is prepended then it is taken as a fixed length to override input lengths. Append unit q if input magnitudes are given in user quantity units and we will scale them to current plot unit for Cartesian vectors (see PROJ_LENGTH_UNIT for how to change the plot unit) or to km for geovectors. In addition, if +c is selected then the vector magnitudes may be used for CPT color-lookup (and no extra data column is required by -C).
+z[scale] - Expects input \(\Delta x, \Delta y\) vector components and uses the scale [1] to convert to polar coordinates with length in given unit. Append unit q if input components are given in user quantity units and we will scale to current plot unit for Cartesian vectors (see PROJ_LENGTH_UNIT for how to change the plot unit) or to km for geovectors. In addition, if +c is selected then the vector magnitudes may be used for CPT color-lookup (and no extra data column is required by -C).
Note: Vectors were completely redesigned for GMT5 which separated the vector head (a polygon) from the vector stem (a line). In GMT4, the entire vector was a polygon and it could only be a straight Cartesian vector. Yes, the old GMT4 vector shape remains accessible if you specify a vector (-Sv|V) using the GMT4 syntax, explained here: size, if present, will be interpreted as \(t_w/h_l/h_w\) or tailwidth/headlength/halfheadwidth [Default is 0.075c/0.3c/0.25c (or 0.03i/0.12i/0.1i)]. By default, arrow attributes remain invariant to the length of the arrow. To have the size of the vector scale down with decreasing size, append +nnorm, where vectors shorter than norm will have their attributes scaled by length/norm. To center the vector on the balance point, use -Svb; to align point with the vector head, use -Svh; to align point with the vector tail, use -Svt [Default]. To give the head point’s coordinates instead of direction and length, use -Svs. Upper case B, H, T, S will draw a double-headed vector [Default is single head]. Note: If \(h_l/h_w\) are given as 0/0 then only the head-less vector stick will be plotted.
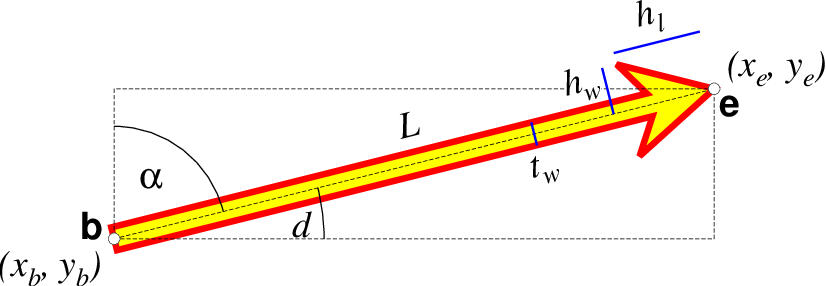
A GMT 4 vector has no separate pen for the stem -- it is all part of a Cartesian polygon. You may optionally fill and draw its outline. The modifiers listed above generally do not apply. Note: While the tailwidth (\(t_w\)) and headlength (\(h_l\)) parameters are given as indicated, the halfheadwidth (\(h_w\)) is oddly given as the half-width in GMT 4 so we retain that convention here (but have updated the documentation; blue lines indicate these three parameters).
Classic Mode Arguments
These options are used to manipulate the building of layered GMT PostScript plots in classic mode. They are not available when using GMT modern mode.
- -K (more …)
Do not finalize the PostScript plot.
- -O (more …)
Append to existing PostScript plot.
- -P (more …)
Select “Portrait” plot orientation.
Examples
Note: Below are some examples of valid syntax for this module.
The examples that use remote files (file names starting with @)
can be cut and pasted into your terminal for testing.
Other commands requiring input files are just dummy examples of the types
of uses that are common but cannot be run verbatim as written.
To draw the vector field given by the files r.nc and theta.nc on a linear plot with scale 5 cm per data unit, using vector rather than stick plot, scale vector magnitudes so that 10 units equal 1 inch, and center vectors on the node locations, run
gmt grdvector r.nc theta.nc -Jx5c -A -Q0.1i+e+jc -S10i > gradient.ps
To plot a geographic data sets given the files comp_x.nc and comp_y.nc, using a length scale of 200 km per data unit and only plot every 3rd node in either direction, try
gmt grdvector comp_x.nc comp_y.nc -Ix3 -JH0/20c -Q0.1i+e+jc -S200k > globe.ps
Vector scaling and unit effects
The scale given via -S may require some consideration. As explained in -S, it is specified in data-units per plot or distance unit. The plot or distance unit chosen will affect the type of vector you select. In all cases, we first compute the magnitude r of the user’s data vectors at each selected node from the x and y components (unless you are passing \((r,\theta)\) grids directly with -A or -Z). These magnitudes are given in whatever data units they come with. Let us pretend our data grids record secular changes in the Earth’s magnetic horizontal vector field in units of nTesla/year, and that at a particular node the magnitude is 28 nTesla/year (in some direction). If you specify the scale using plot distance units (c|i|p) then you are selecting Cartesian vectors. Let us further pretend that you selected -S10c as your scale option. That means you want 10 nTesla/year to equate to a 1 cm plot length. Internally, we convert this scale to a plot scale of 1/10 = 0.1 cm per nTesla/year. Given our vector magnitude of 28 nTesla/year, we multiply it by our plot scale and finally obtain a vector length of 2.8 cm, which is then plotted. The user’s data units do not enter of course, i.e., they always cancel [Likewise, if we had used -S25i (25 nTesla/year per inch) the plot scale would be (1/25) = 0.04 inch per nTesla/year and the vector plot lengths would be 28 * 0.04 inch = 1.12 inch]. If we now wished to plot a 10 nTesla/year reference vector in the map legend we would plot one that is 10 times 0.1 cm = 1 cm long since the scale length is constant regardless of map projection and location. A 10 nTesla/year vector will be 1 cm anywhere.
Let us contrast this behavior with what happens if we use a geographic distance unit instead, say -S0.5k (0.5 nTesla/year per km). Internally, this becomes a map scale of 2 km per nTesta/year. Given our node magnitude of 28 nTesla/year, the vector length will be 28 x 2 km = 56 km. Again, the user’s data unit do not enter. Now, that vector length of 56 km must be projected onto the Earth, and because of map distortions, a 56 km vector will be mapped to a length on the plot that is a function of the user’s map projection, the map scale, and possibly the location on the map. E.g., a 56 km vector due east at Equator on a Mercator map would seem to equal ~0.5 degree longitude but at 60 north it would be more like ~1 degree longitude. A consequence of this effect is that a user who wants to add a 10 nTesla/year reference vector to a legend faces the same problem we do when we wish to draw a 100 km map scale on a map: the plotted length usually will depend on latitude and hence that reference scale is only useful around that latitude.
This brings us to the inverse scale option, -Silength. This variant is useful when providing the inverse of the scale is simpler. In the Cartesian case above, we could instead give -Si0.1c which would directly imply a plot scale of 0.1 cm per nTesla/year. Likewise, for geographic distances we could give -Si2k for 2 km per nTesla/year scale as well. As the -Si argument increases, the plotted vector length increases as well, while for plain -S the plot length decreases with increasing scale.
Notes
Be aware that using -I may lead to aliasing unless your grid is smoothly varying over the new length increments. It is generally better to filter your grids and resample at a larger grid increment and use these grids instead of the originals.