mapproject
Forward and inverse map transformations, datum conversions and geodesy
Synopsis
gmt mapproject [ table ] -Jparameters -Rregion [ -Ab|B|f|F|o|O[lon0/lat0][+v] ] [ -C[dx/dy][+m] ] [ -Dc|i|p ] [ -E[datum] ] [ -F[e|f|k|M|n|u|c|i|p] ] [ -G[lon0/lat0][+a][+i][+uunit][+v] ] [ -I ] [ -Ltable[+p][+uunit] ] [ -N[a|c|g|m] ] [ -Q[d|e] ] [ -S ] [ -T[h]from[/to] ] [ -V[level] ] [ -W[b|B|e|E|g|h|j|m|M|n|o|O|r|R|w|x][+n[nx[/ny]]] ] [ -Z[speed][+a][+i][+f][+tepoch] ] [ -bbinary ] [ -dnodata[+ccol] ] [ -eregexp ] [ -fflags ] [ -ggaps ] [ -hheaders ] [ -iflags ] [ -jflags ] [ -oflags ] [ -pflags ] [ -qflags ] [ -sflags ] [ -:[i|o] ] [ --PAR=value ]
Note: No space is allowed between the option flag and the associated arguments.
Description
mapproject reads (lon, lat) positions from tables [or standard input] and computes (x, y) coordinates using the specified map projection and scales. Optionally, it can read (x, y) positions and compute (lon, lat) values doing the inverse transformation. This can be used to transform linear (x, y) points obtained by digitizing a map of known projection to geographical coordinates. May also calculate distances along track, to a fixed point, or closest approach to a line. Alternatively, can be used to perform various datum conversions. Additional data fields are permitted after the first 2 columns which must have (longitude,latitude) or (x, y). See option -: on how to read (latitude,longitude) files. Finally, mapproject can compute a variety of auxiliary output data from input coordinates that make up a track. Items like azimuth, distances, distances to other lines, and travel-times along lines can all be computed by using one or more of the options -A, -G, -L, and -Z. Note: Depending on the Optional Arguments listed below, most times -J or -R are not actually required.
Required Arguments
- table
One or more ASCII (or binary, see -bi[ncols][type]) data table file(s) holding a number of data columns. If no tables are given then we read from standard input.
(Note that depending on the Optional Arguments listed below, sometimes -J and -R are not actually required.)
Optional Arguments
- -Ab|B|f|F|o|O[lon0/lat0][+v]
Calculate azimuth along track or to the optional fixed point set with lon0/lat0. Choose among several directives:
b - Calculate the back-azimuth from data points to the fixed point.
f - Calculate the forward azimuth from the fixed point to each data point.
o - Get orientations (-90/90) rather than azimuths (0/360).
Upper case directives F, B or O will convert from geodetic to geocentric latitudes and estimate azimuth of geodesics (assuming the current ellipsoid is not a sphere). Note: If no fixed point is given then we compute the azimuth (or back-azimuth) from the previous point. One modifier is available:
+v - Obtain a variable 2nd point (lon0/lat0) via columns 3-4 in the input file.
See Output Order for how -A affects the output record. Note: If -R and -J are given the we project the coordinates first and then compute Cartesian angles instead.
- -C[dx/dy][+m]
Set center of projected coordinates to be at map projection center [Default is lower left corner]. Optionally, add offsets in the projected units to be added (or subtracted when -I is set) to (from) the projected coordinates, such as false eastings and northings for particular projection zones [0/0]. The unit used for the offsets is the plot distance unit in effect (see PROJ_LENGTH_UNIT) unless -F is used, in which case the offsets are in meters. Alternatively, for the Mercator projection only, append +m to set the origin of the projected y coordinates to coincide with the standard parallel [Equator].
- -Dc|i|p
Temporarily override PROJ_LENGTH_UNIT and use c (cm), i (inch), or p (points) instead. Cannot be used with -F.
- -E[datum]
Convert from geodetic (lon, lat, height) to Earth Centered Earth Fixed (ECEF) (x, y, z) coordinates (add -I for the inverse conversion). Append datum ID (see -Qd) or give ellipsoid:dx,dy,dz where ellipsoid may be an ellipsoid ID (see -Qe) or given as a[,inv_f], where a is the semi-major axis and inv_f is the inverse flattening (0 if omitted). If datum is - or not given we assume WGS-84.
- -F[e|f|k|M|n|u|c|i|p]
Force 1:1 scaling, i.e., output (or input, see -I) data are in actual projected meters. To specify other units, append the desired unit (see Units). Without -F, the output (or input, see -I) are in the units specified by PROJ_LENGTH_UNIT (but see -D).
- -G[lon0/lat0][+a][+i][+uunit][+v]
Calculate distances along track or to the optional fixed point set with -Glon0/lat0. If no fixed point is given we calculate accumulated distances whereas if a fixed point is given we calculate incremental distances. You can modify this and other features via some modifiers:
+a - Select accumulated distances.
+i - Select incremental distances.
+u - Append the distance unit (see Units for available units and how distances are computed [great circle using authalic radius]), including c (Cartesian distance using input coordinates) or C (Cartesian distance using projected coordinates). The C unit requires -R and -J to be set and all output coordinates will be reported as projected.
+v - Obtain a variable 2nd point (lon0/lat0) via columns 3-4 in the input file; this updates the fixed point per record and thus the selection defaults to incremental distances.
Notes: (1) If both +a and +i are given we will report both types of distances. (2) See Output Order for how -G affects the output record.
- -I
Do the Inverse transformation, i.e., get (longitude,latitude) from (x, y) data.
- -Jparameters
Specify the projection. (See full description) (See cookbook summary) (See projections table).
- -Ltable[+p][+uunit |c |C]
Determine the shortest distance from the input data points to the line(s) given in the ASCII multisegment file table. The distance and the coordinates of the nearest point will be appended to the output as three new columns. Consider these modifiers:
+p - Report the line segment id seg and the fractional point number pnr instead of lon/lat of the nearest point.
+u - Append the distance unit (see Units for available units and how distances are computed [great circle using authalic radius]), including c (Cartesian distance using input coordinates) or C (Cartesian distance using projected coordinates). The C unit requires -R and -J to be set and all output coordinates will be reported as projected.
Notes: (1) Calculation mode for geographic data is spherical, hence -je cannot be used in combination with -L. (2) See Output Order for how -L affects the output record.
- -N[a|c|g|m]
Convert from geodetic latitudes (using the current ellipsoid; see PROJ_ELLIPSOID) to one of four different auxiliary latitudes (longitudes are unaffected). Choose from these directives:
a - Convert to authalic latitudes.
c - Convert to conformal latitudes.
g - Convert to geocentric latitudes [Default].
m - Convert to meridional latitudes.
Use -I to instead convert from auxiliary latitudes to geodetic latitudes.
- -Q[d|e]
List all projection parameters. To only list datums, use -Qd. To only list ellipsoids, use -Qe.
- -Rxmin/xmax/ymin/ymax[+r][+uunit]
Specify the region of interest. |Add_-R|
- -S
Suppress points that fall outside the region.
- -T[h]from[/to]
Coordinate conversions between datums from and to using the standard Molodensky transformation. Use -Th if 3rd input column has height above ellipsoid [Default assumes height = 0, i.e., on the ellipsoid]. Specify datums using the datum ID (see -Qd) or give ellipsoid:dx,dy,dz where ellipsoid may be an ellipsoid ID (see -Qe) or given as a[,inv_f], where a is the semi-major axis and inv_f is the inverse flattening (0 if omitted). If datum is - or not given we assume WGS-84. -T may be used in conjunction with -R -J to change the datum before coordinate projection (add -I to apply the datum conversion after the inverse projection). Make sure that the PROJ_ELLIPSOID setting is correct for your case.
- -V[level]
Select verbosity level [w]. (See full description) (See cookbook information).
- -W[b|B|e|E|g|h|j|m|M|n|o|O|r|R|w|x][+n[nx[/ny]]]
Report a variety of plot dimensions or map regions in projected or geographic units. No input files are read. With no argument we report the map width and hight. The chosen unit of reported plot dimensions may be changed via -D. For other results, select from these directives:
b - Get the bounding box in longitude and latitude.
B - Same, but get the result in -Rw/e/s/n string format returned as trailing text.
e - Return the coordinates of the rectangular area encompassing the non-rectangular area defined by your -R -J
E - Same, but in -Rw/e/s/n string format returned as trailing text.
g - Output the plot coordinates of the appended map point lon/lat.
h - Only output the height of the map.
j - Output the map coordinates of a reference point by appending its code (with standard two-character justification codes).
n - Same, but appended reference point rx/ry is given as normalized positions in the 0-1 range,.
o - If an oblique domain is set via -Rxmin/xmax/ymin/ymax+uunit then return the diagonal corner coordinates in degrees (in the order llx urx lly ury)
O - Same, but get the equivalent -R string format returned as trailing text.
m - Get the rectangular region in projected plot coordinates instead.
M - Same, but returned in -R string format returned as trailing text.
r - Output the rectangular domain that covers an oblique area as defined by -R -J.
R - Same, but get the result in -R| string format returned as trailing text.
w - Only output the width of the map in current plot units.
x - Output the map coordinates of the specific plot reference point px/py.
Optionally (for e or r), append modifier +n to set how many points [100] you want along each side for a closed polygon of the oblique area instead.
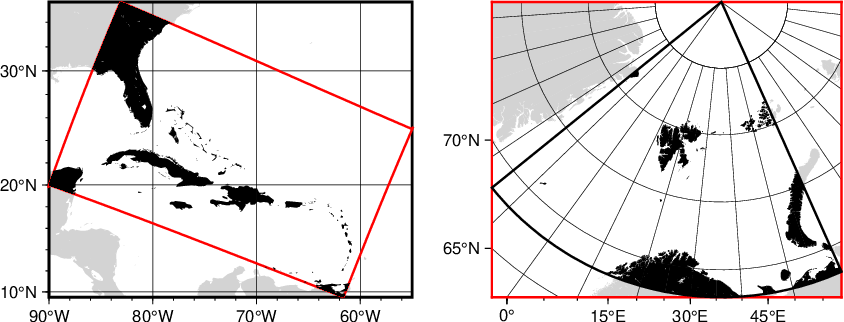
Comparing oblique (red outline) and regular (just meridians and parallels; black outline) regions. (left) Some domains are oblique (their perimeters are not following meridians and parallels). We can use -Wr|R to obtain the enclosing meridian/parallel box or the -R string for that region. (right) Other domains are not oblique but their enclosing rectangular box in the map projection will be. We can explore -We|E to obtain the geographic coordinates of the encompassing oblique rectangle or the -R string for that region.
- -Z[speed][+a][+i][+f][+tepoch]
Calculate travel times along track as specified with -G. Append a constant speed unit; if missing we expect to read a variable speed from column 3. The speed is expected to be in the distance units set via -G per time unit controlled by TIME_UNIT [m/s]. A few modifiers are available:
+i - Output incremental travel times between successive points.
+a - Output accumulated travel times.
+f - Format the accumulated (elapsed) travel time according to the ISO 8601 convention. As for the number of decimals used to represent seconds we consult the FORMAT_CLOCK_OUT setting.
+t - Append epoch to report absolute times (ETA) for successive points. Because of the need for incremental distances the -G option with the +i modifier is required.
Note: See Output Order for how -Z affects the output record.
- -birecord[+b|l] (more …)
Select native binary format for primary table input. [Default is 2 input columns].
- -borecord[+b|l] (more …)
Select native binary format for table output. [Default is same as input].
- -d[i|o][+ccol]nodata (more …)
Replace input columns that equal nodata with NaN and do the reverse on output.
- -e[~]“pattern” | -e[~]/regexp/[i] (more …)
Only accept data records that match the given pattern.
- -f[i|o]colinfo (more …)
Specify data types of input and/or output columns.
- -gx|y|z|d|X|Y|Dgap[u][+a][+ccol][+n|p] (more …)
Determine data gaps and line breaks.
- -h[i|o][n][+c][+d][+msegheader][+rremark][+ttitle] (more …)
Skip or produce header record(s).
- -icols[+l][+ddivisor][+sscale|d|k][+ooffset][,…][,t[word]] (more …)
Select input columns and transformations (0 is first column, t is trailing text, append word to read one word only).
- -je|f|g (more …)
Determine how spherical distances or coordinate transformations are calculated.
- -ocols[+l][+ddivisor][+sscale|d|k][+ooffset][,…][,t[word]] (more …)
Select output columns and transformations (0 is first column, t is trailing text, append word to write one word only).
- -p[x|y|z]azim[/elev[/zlevel]][+wlon0/lat0[/z0]][+vx0/y0] (more …)
Select perspective view.
- -q[i|o][~]rows|limits[+ccol][+a|t|s] (more …)
Select input or output rows or data limit(s) [all].
- -s[cols][+a][+r] (more …)
Set handling of NaN records for output.
- -:[i|o] (more …)
Swap 1st and 2nd column on input and/or output.
- -^ or just -
Print a short message about the syntax of the command, then exit (Note: on Windows just use -).
- -+ or just +
Print an extensive usage (help) message, including the explanation of any module-specific option (but not the GMT common options), then exit.
- -? or no arguments
Print a complete usage (help) message, including the explanation of all options, then exit.
- --PAR=value
Temporarily override a GMT default setting; repeatable. See gmt.conf for parameters.
Units
For map distance unit, append unit d for arc degree, m for arc minute, and s for arc second, or e for meter [Default unless stated otherwise], f for foot, k for km, M for statute mile, n for nautical mile, and u for US survey foot. By default we compute such distances using a spherical approximation with great circles (-jg) using the authalic radius (see PROJ_MEAN_RADIUS). You can use -jf to perform “Flat Earth” calculations (quicker but less accurate) or -je to perform exact geodesic calculations (slower but more accurate; see PROJ_GEODESIC for method used).
ASCII Format Precision
The ASCII output formats of numerical data are controlled by parameters in your gmt.conf file. Longitude and latitude are formatted according to FORMAT_GEO_OUT, absolute time is under the control of FORMAT_DATE_OUT and FORMAT_CLOCK_OUT, whereas general floating point values are formatted according to FORMAT_FLOAT_OUT. Be aware that the format in effect can lead to loss of precision in ASCII output, which can lead to various problems downstream. If you find the output is not written with enough precision, consider switching to binary output (-bo if available) or specify more decimals using the FORMAT_FLOAT_OUT setting.
Examples
Note: Below are some examples of valid syntax for this module.
The examples that use remote files (file names starting with @)
can be cut and pasted into your terminal for testing.
Other commands requiring input files are just dummy examples of the types
of uses that are common but cannot be run verbatim as written.
To transform a remote file with (latitude,longitude) into (x, y) positions in cm on a Mercator grid for a given scale of 0.5 cm per degree and selected region, run:
gmt mapproject @waypoints.txt -R-180/180/-72/72 -Jm0.5c -: > xyfile
To convert UTM coordinates in meters to geographic locations, given a file utm.txt and knowing the UTM zone (and zone or hemisphere), try:
gmt mapproject utm.txt -Ju+11/1:1 -C -I -F
To transform several 2-column, binary, double precision files with (latitude,longitude) into (x, y) positions in inch on a Transverse Mercator grid (central longitude 75W) for scale = 1:500000 and suppress those points that would fall outside the map area, run:
gmt mapproject tracks.* -R-80/-70/20/40 -Jt-75/1:500000 -: -S -Di -bo -bi2 > tmfile.b
To convert the geodetic coordinates (lon, lat, height) in the file old.txt from the NAD27 CONUS datum (Datum ID 131 which uses the Clarke-1866 ellipsoid) to WGS 84, run:
gmt mapproject old.txt -Th131 > new.txt
To compute the closest distance (in km) between each point in the input file quakes.txt and the line segments given in the multisegment ASCII file coastline.txt, run:
gmt mapproject quakes.txt -Lcoastline.txt+uk > quake_dist.txt
Given a file pos.txt with use Cartesian coordinates (say in meters or miles), compute accumulated distance along track with:
gmt mapproject pos.txt -G+uc > cum_distances.txt
Given a file with longitude and latitude, compute both incremental and accumulated distance along track, and estimate travel times assuming a fixed speed of 12 knots. We do this with:
gmt mapproject track.txt -G+un+a+i -Z12+a --TIME_UNIT=h > elapsed_time.txt
where TIME_UNIT is set to hour so that the speed is measured in nm (set by -G) per hour (set by TIME_UNIT). Elapsed times will be reported in hours (unless +f is added to -Z for ISO elapsed time).
To determine the geographic coordinates of the mid-point of this transverse Mercator map, try:
gmt mapproject -R-80/-70/20/40 -Jt-75/1:500000 -WjCM > mid_point.txt
To determine the rectangular region that encompasses the oblique region defined by an oblique Mercator projection, try:
gmt mapproject -R270/20/305/25+r -JOc280/25.5/22/69/2c -WR
To determine the oblique region string (in degrees) that corresponds to a rectangular (but oblique) region specified in projected units defined by an oblique Mercator projection, try:
gmt mapproject -R-2800/2400/-570/630+uk -Joc190/25/266/68/1:1 -WO
To instead get a closed polygon of the oblique area in geographical coordinates, try:
gmt mapproject -R-2800/2400/-570/630+uk -Joc190/25/266/68/1:1 -Wr+n > polygon.txt
To find the region string that corresponds to the rectangular region that encompasses the projected region defined by a stereographic projection, try:
gmt mapproject -JS36/90/30c -R-15/60/68/90 -WE
To obtain the azimuth of a railroad using the points where it enters and leaves a city, try:
echo -87.7447873 42.1192976 -87.7725841 42.1523955 | gmt mapproject -AF+v -fg -o4
Centering Output Region
The rectangular input region set with -R will in general be mapped into a non-rectangular grid. Unless -C is set, the leftmost point on this grid has xvalue = 0.0, and the lowermost point will have yvalue = 0.0. Thus, before you digitize a map, run the extreme map coordinates through mapproject using the appropriate scale and see what (x, y) values they are mapped onto. Use these values when setting up for digitizing in order to have the inverse transformation work correctly, or alternatively, use gmt math to scale and shift the (x, y) values before transforming.
Select Ellipsoidal versus Spherical Solution
GMT will use ellipsoidal formulae if they are implemented and the user have selected an ellipsoid as the reference shape (see PROJ_ELLIPSOID). The user needs to be aware of a few potential pitfalls: (1) For some projections, such as Transverse Mercator, Albers, and Lambert’s conformal conic we use the ellipsoidal expressions when the areas mapped are small, and switch to the spherical expressions (and substituting the appropriate auxiliary latitudes) for larger maps. The ellipsoidal formulae are used as follows: (a) Transverse Mercator: When all points are within 10 degrees of central meridian, (b) Conic projections when longitudinal range is less than 90 degrees, (c) Cassini projection when all points are within 4 degrees of central meridian. (2) When you are trying to match some historical data (e.g., coordinates obtained with a certain projection and a certain reference ellipsoid) you may find that GMT gives results that are slightly different. One likely source of this mismatch is that older calculations often used less significant digits. For instance, Snyder’s examples often use the Clarke 1866 ellipsoid (defined by him as having a flattening f = 1/294.98). From f we get the eccentricity squared to be 0.00676862818 (this is what GMT uses), while Snyder rounds off and uses 0.00676866. This difference can give discrepancies of several tens of cm. If you need to reproduce coordinates projected with this slightly different eccentricity, you should specify your own ellipsoid with the same parameters as Clarke 1866, but with f = 1/294.97861076. Also, be aware that older data may be referenced to different datums, and unless you know which datum was used and convert all data to a common datum you may experience mismatches of tens to hundreds of meters. (3) Finally, be aware that PROJ_SCALE_FACTOR have certain default values for some projections so you may have to override the setting in order to match results produced with other settings. The decision of ellipsoidal (if available) versus spherical is taken in this order:
The user specifies -je which forces the ellipsoidal solution.
The user specifies -jg which forces the spherical solution.
A specific region is set via -R which implies that portions of that region will be more than stated limit of longitude from the specific (or implied if not set) central meridian.
When a spherical solution is requested or implied, we consider the currently selected ellipsoid and substitute the relevant auxiliary latitude as latitude in the exact equation. Finally, coordinate conversion may also be affected by the selected PROJ_SCALE_FACTOR which is typically 0.9996 but is 1 for a sphere. Note: For some projection, a spherical solution may be used despite the user having selected an ellipsoid. This occurs when the user’s -R setting implies a region that exceeds the domain in which the ellipsoidal series expansions are valid. These are the conditions: (1) Lambert Conformal Conic (-JL)and Albers Equal-Area (-JB) will use the spherical solution when the map scale exceeds 1.0E7. (2) Transverse Mercator (-JT) and UTM (-JU) will will use the spherical solution when either the west or east boundary given in -R is more than 10 degrees from the central meridian, and (3) same for Cassini (-JC) but with a limit of only 4 degrees.
Output Order
The production order for the geodetic and temporal columns produced by the options -A, -G, -L, and -Z is fixed and follows the alphabetical order of the options. Hence, the order in which these options appear on the command line is irrelevant. The actual output order can of course be modulated further via -o.
See Also
References
Bomford, G., 1952, Geodesy, Oxford U. Press.
Snyder, J. P., 1987, Map Projections - A Working Manual, U.S. Geological Survey Prof. Paper 1395.
Vanicek, P. and Krakiwsky, E, 1982, Geodesy - The Concepts, North-Holland Publ., ISBN: 0 444 86149 1.